Bölüm 8: Akım Levhaları, Dik Akımlar ve Elektrik Devreleri

8.1 Plazma Akım Levhaları

Akım levhalarının filamentlenmesinden zaten bahsettik. Bu bölüm, Akım levhalarının doğasını ve bunların manyetik alanla ilişkisini inceleyeceğiz.

Bir akım levhası, tam olarak söylendiği gibidir - içinden bir akımın aktığı ince bir yüzey. Açıkça, dağınık bir hareketli yük bulutundan ve silindirik bir akım filamentinden farklıdır. Bir akım tabakası, iki plazma bölgesi arasında, bir şekilde bir Çift Katman gibi bir yüzey oluşturur ve aynı zamanda bir DL (Çift Katman) gibi, genellikle farklı özelliklere sahip bölgeleri ayırır.

Levhadaki akım, tamamen levha içinde bulunan tek yönde akar. Akım, bir dokuma keten tabakasının (woven linen sheet) çözgü ipliklerinde (the warp threads) akıyormuş gibi düşünülebilir: tüm akım, çözgü ipliklerinin her birinde aynı yönde akar ve atkı ipliklerinde (the weft threads) akım akmaz. Elbette bir akım, zıt yönlerde akan iyonlardan ve elektronlardan oluşur, bu nedenle akım tabakası her iki tür parçacığı da içerecektir.

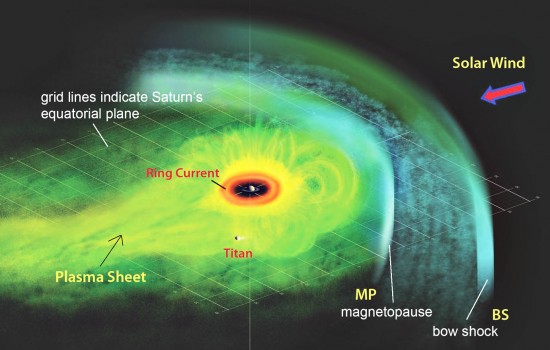
Açıktır ki, tabakanın kendisinin düzlemsel olması gerekmediğinden akımın yönü değişebilir. Örneğin, Dünya'nın manyetosferi ile gelen güneş rüzgârının etkileşime girdiği "pruva şokunda" kısmi küresel bir akım tabakasının açık bir kanıtı vardır.

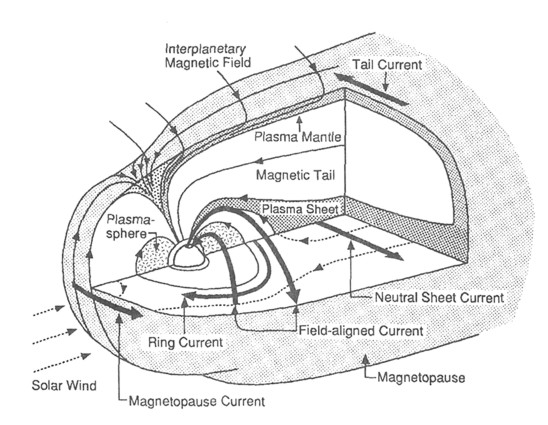
Bir akım tabakasının yakınındaki manyetik alanı analiz edersek, akım tabakasından kaynaklanan manyetik kuvvetin tabakanın her iki tarafında zıt yönlerde olduğunu buluruz. Örneğin, bu sayfadan yukarı doğru bir akım akıyorsa, o zaman sayfanın yukarısında manyetik alan soldan sağa olacak ve sayfanın altında sağdan sola doğru olacaktır, akımın herhangi bir bireysel "dizisi" için sağ el rotasyon kuralından bekleneceği gibi.

(Sağ el döndürme kuralının vektör çarpımı sağ el kuralı ( the vector cross-product right hand rule ) ile aynı olmadığını unutmayın!)

Bu nedenle, bir akım tabakasının temel bir etkisi, karşıt manyetik alanların ayrı alanlarını yaratmaktır. Tabaka konumunun kendisinde, manyetik alan sıfırdır. Bu tam olarak Dünya'nın manyetosferinin uç alanında bulunan durumdur, burada ekvator düzlemindeki bir akım tabakası karşıt manyetik alanın bölgelerini ayırır. Bu durumda, uç tabaka akımı azimutal olarak veya 'batıdan doğuya' akar ve manyetik alanlar radyaldir, Kuzey yarımkürede Dünya'ya doğru ve Güney yarımkürede Dünya'dan uzağa hizalanır.

Kütleçekimi Modeli, her iki taraftaki karşıt manyetik alanların neden olduğu bu akım tabakalarını tanımlar. Manyetik alanların, yüklü parçacıkların yani akımların hareketinin neden olduğu kuvvet alanları olduğunu hatırlayın, Kütleçekimi Modeli bu neden ve etkiyi tersine çeviriyor gibi görünüyor. Akımın yarattığı manyetik alanların aslında yaptığı şey, akımı bir tabaka formuna sıkıştırmaktır. Onlar akımı yaratmazlar.

Bu nedenle akım tabakaları, plazmanın farklı ortamlara tepki olarak hücreselleşebildiği başka bir araçtır.

Akım Tabakaları darbeli plazma itici uygulamasında (pulsed plasma thruster application) kütleyi hızlandırmak için de kullanılabilir. Princeton Üniversitesi Elektrik İtme ve Plazma Fiziği Laboratuvarı'ndan gelen metin ve videoyu buradan(link) izleyin.

8.2 Dikey Akımlar

Akımların manyetik alana (filamentler ve Birkeland Akımları) paralel aktığı ("alanla hizalı" olduğu) ve sıfır alan bölgelerinde (akım levhaları) akımların aktığı durumları halihazırda ele almıştık. Geriye kalan olasılık, akımların manyetik alanla birlikte hareket eden, manyetik olmayan kuvvetlerin etkisi altında, manyetik alana dik bir vektör bileşenine sahip olmasıdır (bkz. Aşağıda 8.3).

[F'nin yüklü bir parçacık üzerinde ortaya çıkan kuvvet vektörü olduğunu hatırlayın; q, parçacık üzerindeki yük miktarının değeridir; E, elektrik alanın belirli bir zaman ve koordinattaki vektör değeridir; U, o andaki yüklü parçacığın hız vektörü ve koordinatıdır ve B, o andaki manyetik alan vektörü ve koordinatıdır. Son olarak, kalın vektörlerin bir skaler büyüklük değerine ve bir yöne, örneğin 3000 km / s doğuya doğru ilerlediğine dikkat edin.]

Yüklü bir parçacık üzerindeki Lorentz Kuvveti, F = q (E + U × B) vektör cebirinde, U parçacığının B manyetik alan hızıyla olan ilişkisine bağlıdır. Vektör çarpımı (vector cross product ) U × B'nin büyüklüğü UBsinθ olarak yazılabilir, burada θ, U ve B arasındaki daha küçük açıdır. U × B tarafından üretilen kuvvetin yönü, sağ yönlü bir vidanın U'dan B'ye çevrilmesi ile verilmektedir, yani hem U hem de B'ye dik açılar

Bu, manyetik alana dik açılarla hareket eden yüklü bir parçacığın alana dik bir düzlemde dairesel bir yol izlemesine neden olur. Buna merkezcil kuvvet diyebiliriz. E sıfır değilse, parçacık ayrıca E yönünde de hızlanacaktır.

Açıktır ki, eğer U sıfırsa veya B'ye paralelse, parçacık üzerinde manyetik alandan kaynaklanan merkezcil bir kuvvet yoktur. Başka bir deyişle, parçacık sabitse veya alana paralel hareket ediyorsa, o zaman manyetik kuvvet parçacığa etki etmeyecektir.

U ve B arasındaki değişken açıları düşünmek yerine, U'nun paralel ve dikey bileşenlerini ayrı ayrı ele almak daha kolaydır. Sadece dik bileşen bir kuvvete neden olduğundan, biz sadece bu bileşene odaklanacağız. Ayrıca aksi belirtilmedikçe E = 0 olarak kabul edeceğiz.

Kuvvetin neden olduğu bir hareket ve bir manyetik alanın kombinasyonundan kaynaklanacak olan parçacık hızı, yönlendirme merkezi denklemi (the Guiding Center Equation) tarafından verilen vp hızıyla manyetik alana dik olarak sürüklenen bir yönlendirme merkezinin etrafındaki dairesel bir hareket olarak düşünülebilir (aşağıdaki resme bakın):

vp = (F × B) / qB2

F'in, yüklü bir parçacığın hareketine neden olan herhangi bir manyetik olmayan kuvvet (örneğin, kütleçekimi veya elektrik alanı) olduğunu unutmayın. Bu hareket daha sonra Lorentz Yasasına göre manyetik alanla etkileşir. Kartezyen koordinatlarda B  z yönünde ve F  y yönünde olduğunda, sonuçta ortaya çıkan hız vp x yönünde olur.

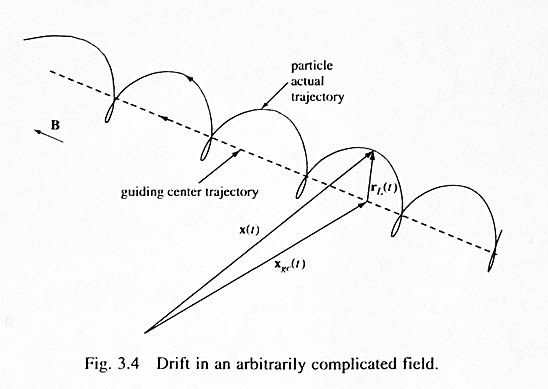
Bu denklemin bize söylediği, bir parçacık manyetik alana dik bir dış kuvvete maruz kaldığında, hem alana hem de kuvvete dik sabit bir vp hızı elde edeceğidir. Bunun nasıl gerçekleştiği şu şekildedir:

Bir parçacık başlangıçta durgunsa, bir dış kuvvet (örneğin bir elektrik alanı) onu Newton yasalarına göre kuvvet yönünde hızlandırmaya başlayacaktır. Bununla birlikte parçacık, manyetik alana dik olarak küçük bir miktar hız veya hız bileşeni kazanır kazanmaz, manyetik alanın sonucu olarak bir merkezcil kuvvet ortaya çıkar ve parçacığın yolunu dış gücün oluşturduğu yörüngeden uzağa çevirmeye başlar.

Dış kuvvet hala parçacığı kuvvet yönünde hızlandırmaya çalışıyor, ancak şimdi merkezcil kuvvetin dış kuvvete karşı çıkan bir bileşeni var. Dış kuvvet yönündeki ivme buna göre azalacaktır.

Dış ve merkezcil kuvvetlerin etkisi altında, parçacık 90 derece dönen eğri bir yol izleyecektir. Yolun dış kuvvete dik olduğu noktada, parçacık yönlendirme merkezi denklemi tarafından verilen vp hızını elde eder ve vp ile B'nin etkileşiminden kaynaklanan merkezcil kuvvet tam olarak dış kuvveti dengeler.

Bu nedenle, artık dış kuvvet yönünde bir ivme olmayacağı gibi, vp yönünde herhangi bir ivme de olmayacaktır çünkü o yönde bir kuvvet yoktur. Parçacık, hem B'ye hem de dış kuvvete dik sabit bir hız kazanmıştır.

Parçacık dikey yönde vp hızıyla hareket etmeye devam ettiği sürece durum sabittir ve dış kuvvet merkezcil kuvvet tarafından dengenir.

8.3 Çeşitli Dış Kuvvetlerin Etkisi

Yukarıda anlatılanlar, bir manyetik alanda bulunan yüklü bir parçacık üzerine etki eden herhangi bir sabit dış kuvvet için geçerlidir. Çeşitli kuvvetler manyetik alana dik yönde hızlara neden olabilir. Bunlara kütleçekimi, bir elektrik alanı ve eylemsizlik kuvvetleri de dahildir. Her birinin, dış kuvvetin parçacığın kütlesinin veya parçacığın yükünün bir fonksiyonu olup olmadığına bağlı olarak aşağıdaki gibi farklı bir etkisi olacaktır:-

Durum A. Elektriksel Alan Kuvveti, FE × B B'ye dik bir elektrik alanı için.

FE = qE olduğundan, yönlendirme merkezi denklemi şöyle olur:

vp = (E x B) / B2

• A Durumunda, dikey hız parçacık üzerindeki yükten bağımsızdır. Bu, filamentli akımlarla maddenin yoğunluğunu (the concentration) değerlendirirken gördüğümüz gibi, iyonların ve elektronların her ikisinin de aynı yönde sürüklendiği özel bir durumla sonuçlanır.

Durum B. Kütleçekimi, Fg×B

Fg = mg olduğundan, sonuçta ortaya çıkan dikey sürüklenme hızı hem parçacıkların kütlesine hem de yüklerine bağlıdır ve Durum B için:

vp = (g × B) × m/qB²

• İyonlar ve elektronlar bu nedenle zıt yönlerde hareket edecek, bu da bir akım, yük ayrımı ve farklı potansiyele sahip bölgeler (yani elektrik alanları) ile sonuçlanacaktır. Tüm bu etkiler, basitçe kütleçekimi ve manyetik alanın etkileşiminin bir sonucu olarak ortaya çıkacaktır. Belli ki bu etkiler daha sonra kendi ikincil etkilerine neden olmaya başlayacak ve bu karmaşık plazma davranışlarını ortaya çıkabilir. (Ref: Fundamentals of Cosmic Electrodynamics, Boris V. Somov, Kluwer Academic Publishers, 1994, Chapter 2, Motion of a Charged Particle in Given Fields)
• Ek olarak, hızın parçacıkların kütlesine bağımlılığı da farklı iyonların kimyasal olarak ayrılmasına veya Marklund Konveksiyonuna neden olabilir.
• Burada özellikle bir durum ilginçtir. Dünya'yı ve manyetik alanını düşünün, bir portakalın parçaları gibi düzenlenmiş yakın uzaya yayılan alan çizgileri olarak görselleştirilebilir. Ekvator düzleminde alan kuzey-güney hizasında olacaktır. Kütleçekimi kuvveti ışınsal olarak (radially) içe ve dolayısıyla alana dik açılarda olacaktır.
• Bu nedenle, örneğin iyonosferin yakın çevresindeki herhangi bir iyon ve elektron, kütleçekimi ve manyetik alanın birleşik etkisi altında hem B hem de g'ye dik hızlar kazanacaktır. İyonların ve elektronların hızları zıt yönlerde olduğundan, bu, ekvator düzlemi etrafındaki bir halkada akan bir akıma eşdeğerdir. Van Allen Kuşağı halka akımlarına örnektir.

• Bu, kütleçekim alanına dik açılarda yönlendirilmiş bir manyetik alanda yüklü parçacıkların varlığının kaçınılmaz bir sonucudur. Bu durumda her zaman bir akım üretilecektir. Jüpiter ve Satürn'ün birkaç uydusu bu durumu gösterir, indüklenen akımların kutup auroral ovallerinin yakınında gezegenlerin atmosferleriyle temas ettiği elektromanyetik ışınımla kanıtlanan bu akımları sergiler. (everal of the moons of Jupiter and Saturn exhibit these currents, evidenced by the electromagnetic radiation where the induced currents come in contact with the planets’ atmospheres in the vicinity of their polar auroral ovals.)

Durum C. Eylemsizlik, Fi = -m (du/dt)   (Newton'un İkinci Hareket Yasası)

Bu durumda, yüklü parçacıkların bir manyetik alanla karşılaştıklarında zaten bir başlangıç ​​momentumu (mu) (eylemsizlik kütlesi çarpı hız vektörü) vardır. yönlendirme merkezi denklemi, ilk momentumun manyetik alan tarafından değiştirileceğini gösterir:

vp = -mq/B² du/dt × B

vp yüke bağlı olduğundan, iyonların ve elektronların son hızı zıt yönlerdedir ve bu nedenle bir akımı temsil eder. Farklı kütlelerdeki iyonlar farklı son hızlar kazanacak ve böylece kimyasal olarak sıralanacaktır. Eylemsizlik etkilerinin bir başka önemli etkisi daha vardır:

• Örneğin, bölgedeki bir I × B kuvveti (aynı dikey doğrultuda zıt yönde hareket eden iyonları ve elektronları hızlandıran) nedeniyle bir plazma hacmi belirli bir hıza hızlandırılırsa, plazma, akımı yönlendiren devre pahasına kinetik enerji kazanmıştır.
• Bu hareketli plazma hacmi daha sonra yerel plazmada bir devre kurabileceği başka bir bölgeye girerse, vp hızı hem B'ye hem de vp'ye dik bir akıma neden olur. Bu akımın B ile etkileşimi, hareketli plazma üzerinde onu yavaşlatan bir kuvvete neden olur. Başka bir deyişle, yeni bir yerde bir akım üretirken plazmanın kinetik enerjisinden tekrar vazgeçilir.
• Bu nedenle, yüklü parçacıkların eylemsizlik hareketi ile bir manyetik alanın etkileşimi, kinetik enerjinin elektromanyetik enerji ile değiş tokuş edilebileceği bir araçtır ve bu nedenle, enerjinin farklı konumlar arasında taşınabileceği bir araçtır.

8.4 Plazmadaki Elektrik Devreleri

Yük bir elektrostatik kaynaktan akmıyorsa veya bir çukura akmıyorsa, kapalı devrenin bir parçasını oluşturacaktır. Uzayda, iletkenler genellikle görünmez (ya da gizli) olduğu ve etki alanlarından çok uzak mesafelerde devreyi kapatabileceği için devre her zaman açık olmayabilir, ancak bir yere kapanmaları gerekir.

Uzaydaki devrelerin dikkate alınması, araştırılan bölgede algılanabilir elektriksel aktiviteyi harekete geçiren enerjinin bir alandan diğerine taşınması gibi davranışları açıklayabilir.

Bu bağlamda, hafif yük dengesizliğine sahip herhangi bir bölge içeren bir plazma, bir manyetik alandaki başka bir plazma bölgesine göre hareket ediyorsa, birinci bölgenin, elektromanyetik alanlar ve kuvvetlerin etkileşimi nedeniyle ikinci bölgede bir elektrik alanı ve akımları indükleyeceğini belirtmekte fayda var.

Kütleçekimi Modeli, yüklü bir cisim etrafında bir Debye kılıfına neden olan benzer etkilere bağlı olan Debye taramasının (Debye screening), yük dengesizliklerinin kapsamını Debye uzunluğuyla sınırlandırdığını kabul eder. Bununla birlikte, Lorentz denkleminden gelen v × B kuvveti, Debye uzunluğundan bağımsızdır ve plazmanın başka bir bölgesinde Debye sınırının çok ötesinde bir elektrik alanı indükleyebilir.

8.5 Devre Elemanları Olarak Çift Katmanlar

Herhangi bir Çift Katman, DL'deki potansiyel düşüş nedeniyle iyonları ve elektronları hızlandırır. DL akım taşıyan bir DL ise, akımın aktığı bir elektrik devresinin etkin bir parçasını oluşturur. Parçacıkları hızlandıracak enerji devre tarafından sağlanır ve DL içinde kinetik enerjiye dönüştürülür.

Bu nedenle DL, eylemsiz bir direnç olarak hareket eder ve konumunun kaymasına neden olan bir tepki yaşayabilir. Bu, güç kaynağı merminin kütlesini hızlandırdığı için bir silahın geri tepmesine benzer. DL tarafından hızlandırılan parçacıklar, çevredeki plazma üzerinde etkileşime girip ışınıma neden olarak bir basınca neden olur. Fazla enerjinin bu şekilde dağıtılması, gerekli mekanizmayı sağlayan bir DL oluşumu yoluyla plazmanın kararlı bir duruma ulaşmasına izin verebilir.

8.6 Enerji ve İndüktans

DL'ye sağlanan devre enerjisi, manyetik alanda depolanan enerjiden veya yığın plazmanın kinetik enerjisinden kaynaklanabilir. Devre terimleriyle, enerji depolayan bir eleman bir indüktördür. Bu nedenle plazma, basit bir devredeki bir indüktöre benzer olarak düşünülebilir. Benzer şekilde, DL, artan akımla azalan direnç dahil olmak üzere değişken özelliklere sahip olmasına rağmen, bazı açılardan bir kapasitör gibi davranır.

Endüktansa sahip tüm elektrik devreleri, devre etrafındaki voltaj, endüktans, direnç ve kapasitans değerlerine bağlı olarak potansiyel olarak kararsızdır. Devrenin toplam direnci negatifse, ki bu genellikle I-V (akım-gerilim) eğrisinin düşen özelliği nedeniyle plazmada söz konusudur, o zaman endüktif devrenin kararlılığı imkansızdır. Gerilim, endüktans ve negatif direnç içeren basit bir devre ya salınır ya da tüm enerjisini dağıtır ve soyu tükenir.

DL'deki potansiyel düşüş plazma potansiyelinden daha büyükse, DL güçlü bir DL olarak sınıflandırılır. Güçlü bir DL, DL'ye plazma potansiyelinden daha düşük enerjilerle yaklaşan parçacıkları yansıtacaktır. Yalnızca plazma potansiyelinin üstünde enerjiye sahip parçacıklar DL'ye girecek ve voltaj farkıyla, yani elektrik alanıyla hızlandırılacaktır.

Bir CCDL'deki plazmanın davranışı, bu nedenle, CCDL'nin oluşumunu yönlendiren harici devrenin özelliklerine bağlıdır.

8.7 Rezonans Devreleri

Endüktans ve kapasitans içeren bir devre, elektriksel olarak salınacağı doğal veya rezonans bir frekansa sahiptir. Benzer şekilde, depolanmış manyetik enerji biçiminde endüktans içeren bir plazma devresi ve negatif direnç sergileyen bir CCDL, DL'deki elektrik alanı ile plazmadaki manyetik alan arasında enerjinin değiş tokuş edildiği bir rezonans frekansına sahip olma eğiliminde olacaktır. DL'deki elektrik alanı arttıkça, DL parçacıkları normal şekilde daha yüksek enerjilere hızlandıracaktır.

Bu modelin, yüksek frekanslı radyasyon (Işıma) patlamaları üretmenin etkili bir yolu olduğu açıktır. Buna karşılık, kütleçekimi modeli, yaygın olarak gözlemlenen bu fenomeni açıklamak için saniyede binlerce kez dönen çok yüksek yoğunluklu nötron yıldızlarını varsayar.

Tüm durumlar bir rezonans frekansı ile sonuçlanmaz. Varyasyonlar genellikle geniş bir frekans bandı üzerinde salınımlara neden olur. DL daha sonra elektrik devresi terimleriyle "gürültülü" olur. Gürültünün etkisi, DL tarafından hızlandırılan ışında bir dizi elektron enerjisi yaratmaktır. Bazı elektronlar, akımı sınırlayan manyetik alandan çıkmak için yeterli enerjiye sahiptir ve bu, plazmanın genişlemesine yol açabilir.