Bölüm 4: Elektromanyetizma

 4.1 Elektromanyetik Alan Denklemi

Bilim insanları, fiziksel sistemleri sistemin davranışını tanımlayan ve tahmin eden matematiksel modellerle açıklamaya çalışırlar.Örneğin Kepler, gezegenlerin hareketini üç yasasıyla açıklamıştır. Aynı şekilde, plazma davranışı, yüklü parçacıkların hareketlerini ve bunların elektrik ve manyetik alanlarla etkileşimlerini tanımlayan elektromanyetik alan denklemleri tarafından yönetilir.

Elektromanyetik alan denklemlerinin iki bileşeni vardır: Maxwell Denklemleri ve Lorentz Kuvvet Yasası. İki bileşen, bir geri besleme döngüsü ile birlikte hareket eder:

Maxwell Denklemleri, yüklü parçacıkların konumuna ve hareketine bağlı olarak elektrik ve manyetik alanları belirler. Ayrıca, eğer biri değişiyorsa elektrik ve manyetik alanların etkileşimini de belirlerler.

Lorentz Kuvvet Yasası, alanlar içinde hareket eden yüklü bir parçacık üzerindeki elektrik ve manyetik kuvvetleri belirler. Bu kuvvet, her parçacığın Newton Yasalarına göre hareket etmesine (hızlanmasına) neden olacaktır. Yüklü parçacıkların konumlarındaki ve hareketlerindeki değişiklikler de elektrik ve manyetik alanlarda değişikliklere neden olur.

Plazmalardaki bu etkileşimli fenomeni takip etmek için bilgisayar programları oluşturulmuştur. Tipik olarak, her biri çok kısa bir süreyi temsil eden bir dizi adım içerirler. İlk olarak, mevcut manyetik ve elektrik alanların durumu ve Lorentz Kuvvet Yasası kullanılarak her parçacığın kütlesi, yükü, hızı ve yönü verildiğinde, her parçacığın bulunduğu konumdaki alan değerleriyle (x, y, z koordinatları) hesaplanır.

Katkıda bulunan kuvvetlerin vektörel toplamı hesaplanır ve parçacığın sonuçta ortaya çıkan ivmesi, parçacığı küçük zaman adımı (Newton'un Hareket Yasaları) aralığında bir yönde küçük bir mesafe hareket ettirir. Bu, tüm parçacık seti için uygulanır.

Daha sonra, her bir parçacığın yeni koordinatları ve kinematik koşulları dikkate alınarak, Maxwell denklemleri elektrik ve manyetik alanların değerlerini belirlemek için kullanılır. Bundan sonra, program, her bir parçacığa etki eden elektrik ve manyetik kuvvetlerin Lorentz Yasası kullanılarak bir kez daha hesaplandığı ilk adıma geri döner.

Döngü, programın belirli bir tekrar sayısı gibi tanımlanmış bir koşula ulaşıldığında veya değişkenlerde belirli bir değere ulaşıldığında, değiştiğinde, aşıldığında veya bir tür hatayla karşılaşıldığında ve bunun gibi durumlarda durmaya yönlendirilmesi ile kontrol edilir.

Bir dizi başlangıç ​​koşulu tanımlandıktan sonra (parçacıkların sayısı, yükleri, kütleleri, başlangıç ​​hızları ve tanımlanmış bir uzay hacmi boyunca varsayılan elektrik ve manyetik alanların yoğunluklarının bir açıklaması), yukarıdaki döngü sürecinin ana hatları aşağıdaki gibi çizilebilir:

1. Lorentz Yasası ile her parçacığa etki eden tüm kuvvetleri hesaplayın
2. Newton'un Hareket Kanunlarını kullanarak çok kısa bir zaman artışıyla yeni konumları ve hızları hesaplayın
3. Bu zaman artışından sonra her yüklü parçacığın yeni konumunda E ve B'yi hesaplayın
4. Bir Bitiş Döngüsü koşulu henüz karşılanmadıysa, 1'e geri dönün ve hesaplamaya devam edin

Daha fazla doğruluk veya "gerçekliğe" daha iyi bir yaklaşım için parçacıkların çarpışması, viskoz ve yerçekimi kuvvetleri gibi başka hususlar da eklenebilir. Bu karmaşık bir girişimdir ve birçok parçacığa sahip büyük modellerin çalıştırılması aylar sürebilir.

Bu geri bildirim döngüsü, hızla matematiksel olarak modellemesi son derece zor olan oldukça karmaşık davranışlara yol açabilir. Basitleştirmeler sıklıkla kullanılır. Bununla birlikte, varsayımların basitleştirilmesi, çoğu kez, plazma davranışını bir gaz veya başka bir akışkanın davranışından ayıran tam olarak bu tür davranışların ihmal edilmesine yol açar.

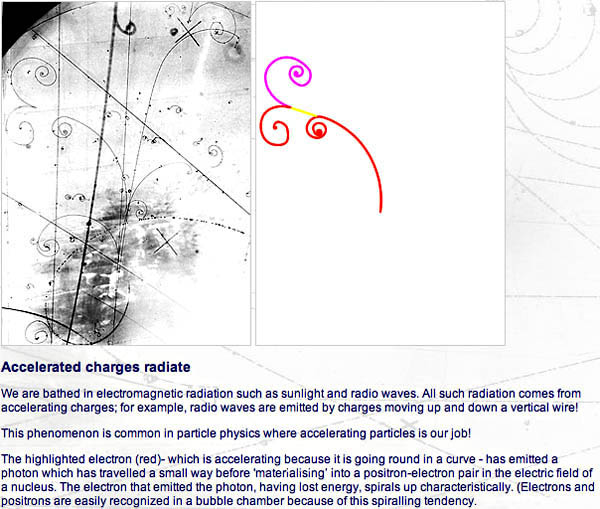
Manyetik alan içindeki bir kabarcık odası, bir parçacık hızlandırıcı ile aynı hizada kurulduğunda parçacık enerjilerinin, etkileşimlerin ve çarpışma yan ürünlerinin değerlendirilmesine olanak tanıyan yüklü parçacıkların görünür izlerini oluşturur.

Bubble chamber tutorial by CERN(link yok)

Elektromanyetik alan denklemlerinin tam bir açıklaması Ek II'de(link?) bulunabilir. Aşağıda, kilit noktaların bir özeti verilmektedir.

4.2 Maxwell Denklemleri

Maxwell Denklemlerinin ve temeldeki araştırmanın etkileri şunlardır:

1. Manyetik alan olmadığında statik bir elektrik alanı mevcut olabilir; Örneğin, bir kapasitör veya statik yüklü Q bir toz parçacığı, manyetik alanı olmayan bir elektrik alanına sahiptir.
2. Elektrik alanı olmadan sabit bir manyetik alan var olabilir; Örneğin, sabit akımı I olan bir iletken, elektrik alanı olmayan bir manyetik alana sahiptir.
3. Elektrik alanların zaman değişkeni olduğunda, sıfır olmayan bir manyetik alan mevcut olmalıdır.
4. Manyetik alanların zaman değişkeni olduğunda, sıfır olmayan bir elektrik alanı mevcut olmalıdır.
5. Manyetik alanlar, kalıcı mıknatıslar dışında yalnızca iki şekilde üretilebilir: bir elektrik akımı veya değişen bir elektrik alanı ile.
6. Manyetik tek kutuplar var olamaz; tüm manyetik akım hatları kapalı döngülerdir.

4.3 Lorentz Kuvvet Yasası

Lorentz Kuvvet Yasası, hem elektrik hem de manyetik alanlara maruz kalan yüklü bir parçacık üzerindeki toplam kuvveti ifade eder. Ortaya çıkan kuvvet, yüklü parçacığın hareketini Newton mekaniği tarafından belirler. Lorentz denklemi tüm plazma davranışları için temel olduğundan, ne anlama geldiğini anlamak için biraz zaman harcamaya değer. Denklem:

F = Q(E + U × B)

(Vektörler kalın yazı ile verilmiştir ve aşağıda açıklanmıştır.)

Burada F, parçacık üzerindeki Lorentz kuvvetidir; Q, parçacık üzerindeki yüktür; E, elektrik alan yoğunluğudur; U, parçacığın hızıdır; B manyetik akım yoğunluğudur ve "×" vektörel çapraz çarpım simgesidir, yalnızca bir çarpma işareti değildir. "U çarpı B" olarak okuyun.

Denklemin gerçekte ne anlama geldiğini anlamak için vektörler hakkında biraz bilgi sahibi olmamız gerekir.

Bir vektör, hem büyüklüğü hem de yönü olan bir niceliktir. Örneğin hız ve kuvvet vektöreldir. Bir ok gibidir: Bir uzunluğu vardır ve bir yönü işaret eder. Buna karşılık, bir skaler niceliğin yalnızca büyüklüğü vardır. Örneğin sürat ve sıcaklık skalerdir. Vektör cebiri, vektörlerle ilgilenen matematiktir. Bilmek isteyenler için, vektör cebiriyle ilgili daha fazla ayrıntı Ek III'te(link) verilmiştir. Hiperfizik(link??) açıklaması da iyi bir giriş niteliğindedir. Lorentz denklemini anlamanın esasları burada açıklanacaktır.

İlk olarak, bir vektörü skaler bir miktarla çarpmak, birkaç benzer oku uçtan uca yan yana koymak gibidir. Vektör birinci oktur; skaler miktar, benzer okların sayısıdır. Sonuç, orijinal vektörle aynı yönde daha büyük bir oktur.

Basitleştirilmiş bir örnek, bir arabanın hızını, düz bir çizgide hareket ederken başlangıç ​​hızının üç katına çıkarmaktır. Arabanın hız vektörünün, tabanı veya başlangıç ​​noktası her zaman arabanın merkezinde olan, yolun tam aşağısını gösteren bir ok olduğunu hayal edin. Bu oku 20 km / saatlik bir başlangıç ​​hızını temsil edecek şekilde 20 cm uzunluğunda hayal edin. Ardından, arabanın tekerleklerinin daha hızlı dönmesini sağlamak ve aracı daha yüksek bir hıza çıkarmak (hızlandırmak) için gaz pedalına bastırırsınız. Araba hızlandıkça, okun uzunluğu her zaman aracın hızına uyacak şekilde artar. 60 km / saat hızda ok 60 cm uzunluğundadır ve yönü hala yola paraleldir. Fren pedalına basarsanız, araç ters yönde hızlanır, yavaşlar ve ok kısalır ve kısalır. Araba durduğunda, hızı sıfıra düşer ve hız okunun veya vektörünün uzunluğu sıfır olur.

"Bunu anlamak kolay" diyorsunuz. "Direksiyonu, diyelim ki sola çevirirsem ne olur?" Bu tür bir hareket, arabanın merkez hattına paralel olan yönden farklı bir yönde arabaya ek bir kuvvet uygular. Hızını artırmaz veya azaltmaz (sürtünmeyi ihmal ederek!) Ama araba döndüğü için bir şeyler değişir! Tekerleklerden 60 km / saat gitmesini sağlayan hız vektörünün uzunluğu değişmedi, ancak farklı bir yönde ek bir kuvvet uygulandı, bu nedenle şimdi hız vektörü iki farklı kuvvetin sonucu haline geldi (merkeze etki eden iki ok) araba). Direksiyonu aynı açıda tuttuğunuz sürece, arabayı döndürmek isteyen aynı kuvvet uygulanır ve sabit bir hızla bir daire üzerinde hareket eder.

İki tür hızlanma olduğunu görebilirsiniz: hareketin hızındaki değişimler (yavaş ya da hızlı) ve hareketin yönündeki değişimler. Her iki tür değişim de bir nesneye uygulanan bir kuvvetin sonucudur.

İki vektörü birlikte çarpmak biraz daha karmaşıktır. Baştaki yuvanın birinci vektörü temsil ettiği ve ikinci vektörün tahtaya çizildiği ahşap bir tahtadaki çok büyük bir vidayı düşünün. Vida, yuva ikinci vektörle aynı hizaya gelene kadar saat yönünde döndürüldüğünde, vida hem yuvaya hem de ikinci vektöre dik açılarla kartın içine hareket edecektir. Hareket miktarı vidanın boyutlarına ve döndürülme miktarına bağlıdır. Vektör çapraz çarpımı biraz buna benzer.

Daha ayrıntılı bilgi için: https://youtu.be/7oYrMMdb9lI

Çapraz çarpımı kullanarak iki vektörün birlikte çarpılması, önceki iki vektörün her ikisine de dik açıda olan başka bir vektörle sonuçlanır - yani, önceki iki vektörü içeren düzleme dik. Yeni vektörün yönü, hayali vidamızın hareket yönü ile verilmektedir. Yeni vektörün büyüklüğü (uzunluğu) hem döndürülen açıya hem de orijinal vektörlerin boyutuna bağlıdır.

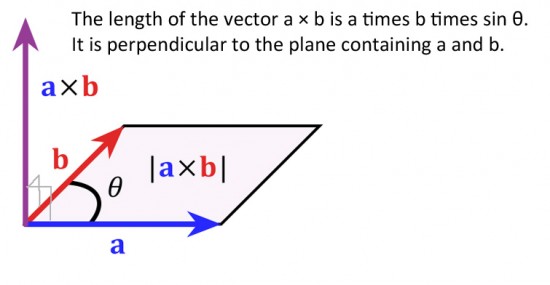
Vidamızda olduğu gibi, ilk etapta vektörler hizalanırsa (paralel şekilde), o zaman vida hareket etmez. Paralel hizalanmış vektörlerin çapraz çarpımı sıfırdır.

Daha resmi olarak, Kartezyen koordinatlarda, x yönündeki bir vektör, y yönündeki bir vektörle çaprazlanırsa, sonuç z yönündeki bir vektördür. Elde edilen vektörün büyüklüğü, iki orijinal vektörün uzunluklarının ve aralarındaki daha küçük açının sinüsünün üçlü çarpımıdır. Paralel ise aralarındaki açı sıfırdır. Sinüs (0 °) sıfır olduğunda, z yönünde ortaya çıkan bir kuvvet olmaz.

Etki, dönen katı maddelerdeki jiroskopik etkiye(link) çok benzer: bir yöndeki kuvvet, dik açılardaki bir yönde harekete neden olur. Bu devinim olarak bilinir.

Lorentz Kuvvet Yasasına geri dönersek, toplam kuvvetin iki kısımdan oluştuğunu görüyoruz. İlk kısım, parçacık üzerindeki yükün skaler değerinin ve elektrik alan kuvvet vektörünün çarpımı olan QE'dir. Elektrik alandan kaynaklanan kuvvetin büyüklüğü, parçacık üzerindeki yük ile elektrik alanın kuvvetinin çarpımıdır.

Elektrik alandan kaynaklanan kuvvetin sabit ve E'nin yönünde olduğuna dikkat edin, dolayısıyla parçacık Newton'un hareket yasasına göre pozitif yük için E'nin yönünde hızlanacaktır, ve negatif yük için ters yönde.

Denklemin ikinci bölümü olan Q(U × B) daha ilginçtir. Burada, çapraz çarpım kullanılarak çarpılan ve daha sonra parçacık üzerindeki yük ile çarpılan iki vektörümüz var. Parçacığın alanla hizalı olarak hareket etmediğini varsayarsak, kuvvet sıfır olduğunda, sonuç hem parçacığın hareket yönüne hem de manyetik alana dik açılarda olan bir kuvvet olacaktır. Sağ El Kuralı (linkle:https://tr.wikipedia.org/wiki/Sa%C4%9F_el_kural%C4%B1), manyetik bir alanın belirli bir yönde alana giren yüklü bir parçacık üzerine uyguladığı "yönlendirme" kuvvetini açıklayacaktır.

Harekete dik açı yapan bir kuvvet merkezcil bir kuvvettir (https://tr.wikipedia.org/wiki/Merkezcil_kuvvet#:~:text=Merkezcil%20kuvvet%2C%20dairesel%20hareket%20s%C4%B1ras%C4%B1nda,y%C3%BCzden%20bir%20merkezcil%20ivme%20olu%C5%9Fur.) (tanım: "merkeze doğru"). Manyetik alan bu nedenle yüklü parçacığın manyetik alanın yönüne dik bir düzlemde bir daire içinde hareket etmesine neden olacaktır. Parçacık çember etrafında hareket ederken, herhangi bir noktadaki hızı hala manyetik alana dik açılarda bir bileşene sahip olacaktır ve bu nedenle yine de çember içinde hareket etmesini sağlayan merkezcil bir kuvveti deneyimleyecektir. Yönü sürekli değişmektedir, ancak bu koşul altında skaler hızı (m / s) değişmez.

Basit bir durum, hareketli ve yüklü bir parçacık (sabit) bir manyetik alana girdiğinde ne olacağını düşünmektir. Basit olması için, parçacığın manyetik alana uygulayabileceği tüm etkileri göz ardı edeceğiz. Alanın yönüne paralel olarak alana girerse, hiçbir kuvvet yaşamaz ve hızı (skaler hız veya yönü) değişmez. Alana, alanın yönüne dik bir açıyla girerse, yolu basitçe kendi üzerine kapanan bir daire şeklinde kıvrılır.

Bir elektrik alanı olmadan, Lorentz yasası (merkezcil kuvvet) F = Q (U × B) olur. Yüklü parçacığa uygulanan kuvvet, parçacığın yükü olan Q ile, U, hız vektörü ve manyetik alan vektörü olan B ile doğru orantılıdır. U × B'nin anlamı, iki vektör arasındaki daha küçük açının sinüsünün U çarpı B çarpıdır; bu, UB'nin bir açının sinüsü ile çarpıldığı, dolayısıyla etkisinin sıfırdan 1'e kadar değiştiği anlamına gelir. (U X B = U.B.sinƟ) Aşağıdaki karşılaştırmalı gösterimde, parçacığın yükü ve manyetik alan sabit tutulur ve parçacığın alana girerken hızı soldan sağa doğru artar. Parçacık ne kadar hızlı hareket ederse, ortaya çıkan dairesel hareketin yarıçapı o kadar büyük olur, çünkü r yarıçapı, parçacığın doğrusal momentumunun mU ölçüsüdür, burada m, parçacık kütlesidir: r = mU÷(|Q|B). Diğer iki değişken sabit tutulurken yük artarsa ​​aynı sonuç geçerli olacaktır.

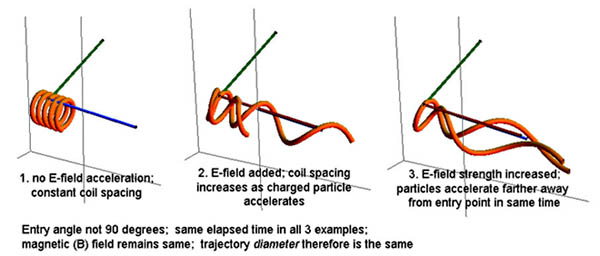
Yüklü parçacık manyetik alan yönüne sıfır ile 90 derece arasında bir açıyla girerse alan, parçacığı dairesel bir harekete zorlarken, alana paralel yönde "sürüklenecek" . Bu "sürüklenen" dairesel yol, bir sarmalın izini sürer. Çemberin "kılavuz merkezi" manyetik alanın alan çizgisini takip eder. Yarıçap r, Larmor yarıçapı veya siklotron yarıçapı olarak bilinir. Aşağıdaki üç resimde, parçacığın giriş açısı ve manyetik alanın kuvveti B, sağa doğru küçük bir sürüklenme hareketi ile aynı kalır. İlk giriş hızı, yüklü bir parçacığın manyetik alana ne kadar hızlı girerse, eğrilik yarıçapı o kadar büyük olduğunu göstermek için soldan sağa doğru adım adım artırılır.

Aşağıdaki görüntü serisinde, manyetik ve elektrik alan çizgilerine dokunan yeşil giriş vektörü, pozitif yüklü bir parçacığın (ortak düşünceye göre) alanlara "girerken" hangi yönde hareket ettiğini gösterir. Parçacık, girişte bu vektör çizgisi boyunca her iki yönde de gidebilir, bu nedenle göreceğiniz gibi yeşil vektörün ucundan çıkan iki yörünge vardır. Parçacık negatif yüklü olsaydı, ters yönde hızlanırdı ve daha ağır olsaydı veya daha hızlı hareket ederse, tasvir edilenden daha büyük bir çap dairesine sahip olurdu. Benzer şekilde, manyetik veya elektrik alanlar değiştirilirse, diğer faktörler sabit tutulursa, bu da benzer şekilde parçacığın davranışını değiştirir. Dar turuncu "tüpler", partikülün giriş koşullarından kaynaklanan yörüngesini temsil eder.

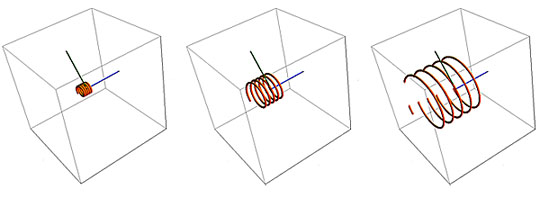
Yüklü bir parçacık düzgün bir B manyetik alanına girdiğinde, yolu, yarıçapı r, doğrusal momentumuyla, kütle çarpı hızıyla (mU) orantılı olan bir daireye bükülür. Parçacığın hızı değişmez, dolayısıyla kinetik enerjisi değişmez ve alan parçacık üzerinde iş yapmaz. Bu, yerçekiminin uzayda yörüngedeki bir uyduya sürekli bir merkezcil kuvvet uygulamasına benzer. Manyetik alan yönü mavi bir eksenel çizgiyle gösterilir; yeşil bir radyal çizgi ile de partikül giriş açısı.

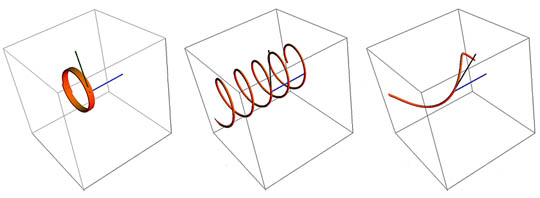
Parçacığın B alanına giriş açısı dikten paralele değişirken, yörüngesi spirale dönüşecektir. Açı 90 dereceden manyetik alan yönüne düştükçe ve alana sıfıra veya paralel olmaya yaklaştıkça spiral yarıçapta azalacaktır. Yeşil giriş vektörünün değişen açısına, soldan sağa ve sarmal uzamaya dikkat edin.

Yukarıdaki resimle Mathematica Demonstrations ile oluşturuldu.

Toplam kuvvet, elektrik ve manyetik kuvvetlerin vektörel bileşimi olacaktır ve iki alan arasındaki açıya bağlıdır (alakalı resimler aşağıda).

Elektrik ve manyetik alanlar paralel ise (alanla hizalı akım durumunda olduğu gibi daha sonra ele alacağız), alanların eksen yönüne radyal olarak yaklaşan yüklü bir parçacık, alanların yönüyle hizalı sarmal bir yolda hareket etmek için sınırlandırılacaktır. Yani, parçacık Lorentz kuvvetinin bir sonucu olarak hızlanacak (yönünü sürekli olarak manyetik alanın eksen yönü etrafında spiral olarak değiştirecek) ve aynı anda elektrik alanı yönünde hızlanacaktır (skaler hızını değiştirecektir). Bu, parçacığın Elektrik alanı yönündeki hız bileşeni zamanla arttıkça birbirini izleyen devirleri gitgide daha uzak hale getirir.

Bu alanla hizalı durumda (E ve B alanları paralel) bir parçacık yörüngesi, E-alan vektörünün (kırmızı) eksenel olarak hızlanmaya zorlamasıyla aynı zamanda uygulanan merkezcil daireselleştirici manyetik kuvvete sahiptir. Zamanla parçacık neredeyse alanlara paralel hareket eder.

Yüklü parçacık birleştirilmiş, hizalanmış alana eksenel olarak (manyetik alana paralel) girerse, manyetik alana maruz kalmaz, bu nedenle bir kılavuz merkez etrafında dönme kuvveti uygulanmaz. Ancak elektrik alan, parçacığı alan çizgileri boyunca hızlandırmaya devam edecektir. Yüküne bağlı olarak, parçacık hızlanma kuvveti yönünde girerse, hızı artar. Bu kuvvete karşı girerse yavaşlar ve durup ters yönde tekrar hızlanabilir. Bir elektrik alanının "yönünün" kuvvetinin pozitif yüklü bir parçacığa uygulandığı yön olarak tanımlandığını hatırlayın.

Alanlar hizalı değilse, yükün özelliklerine, alan kuvvetlerine, giriş yönüne ve manyetik ve elektrik alanların açısal yanlış hizalamasına bağlı olarak çeşitli yörünge kombinasyonları oluşabilir.

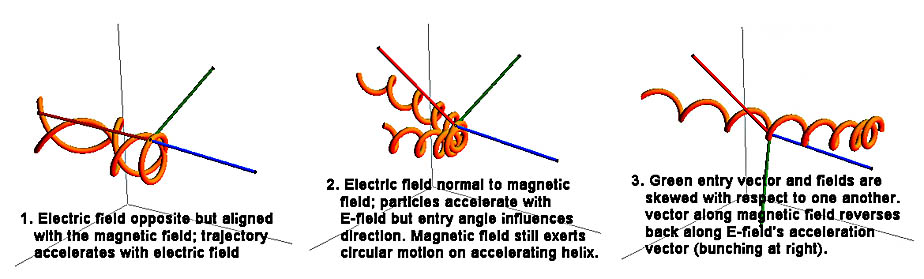
Sabit bir elektrik alanı mevcut olduğunda, genel eğilimi, kendi alan çizgileriyle daha yakın hizalanmış parçacıkları hızlandırmak ve hızları artırmak olacaktır. Mathematica Demonstrations ile oluşturulan yukarıdaki resimler

Bu yörüngeler karmaşık görünse de, bir seferde aynı giriş hızına sahip sabit elektrik ve manyetik alanlara sahip tek bir yüklü parçacık içerirler. Pratikte, farklı polaritelere ve hız vektörlerine sahip birçok yüklü parçacık, aynı anda bir hacimde yer kaplayabilir ve bunların elektrik ve manyetik etkileşimleri, içinde hareket ettikleri alan değerlerini etkileyecektir.

Ayrıca, tümü plazma etkileşimlerine başka kuvvetler (yerçekimi, viskoz, çarpışmalar) uygulayabilen toz, tanecik ve büyük cisimlerin yanı sıra nötr parçacıklar da olabilir.

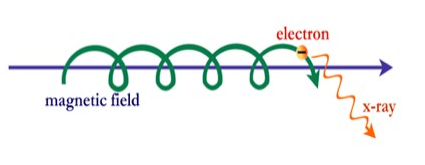
alan-hizalı göreli elektron üreten X-ışını dalga boyu senkrotron radyasyonu

Uzayda manyetik alan çizgileri etrafında spirallenen göreceli elektronların ikincil etkilerinin genellikle senkrotron radyasyonu şeklinde tespit edildiğini not ediyoruz. Lorentz Kuvvet Yasası göz önüne alındığında, bu nedenle manyetik alanla hizalı bir elektrik alanı olması gerektiğini ve manyetik alana paralel bir hız bileşeni ile spiral elektronların eksenel hareketinin alanla hizalı bir akım oluşturduğunu biliyoruz. Bu akımlar Birkeland akımlarıdır; birçok kozmik ölçekte meydana gelirler.

4.4 Alan Denklemlerinin Diğer Etkileri

Elektromanyetik alan denklemlerinin uygulanmasından kaynaklanan bazı temel sonuçları hatırlamakta fayda var.

1. Elektrik alanları, tüm yüklü parçacıklar üzerinde bir kuvvet oluşturur.
2. Elektrik kuvveti, zıt yüklü parçacıklar için zıt yönlerde olacaktır; bu nedenle, bir elektrik alanı, zıt hızlarda iyon ve elektron üretecek ve bu nedenle onları ayırma eğiliminde olacaktır. Uzayda yük ayrımı plazma fiziğinde önemlidir.
3. Manyetik kuvvetin yönü momentuma ve yüke bağlıdır; iyonlar ve elektronlar bu nedenle farklı yarıçaplar ve dönme süreleri ile zıt yönlerde daire çizeceklerdir.
4. Bir manyetik alan yönünde hareket eden toplu plazma, yüklü parçacıklar üzerinde yeni kuvvetlere neden olacak yerel bir elektrik alanının gelişmesine neden olacaktır.
5. Yüklü parçacıkların dağılımındaki değişiklikler, aralarındaki elektrik alanında bir değişikliğe neden olur; değişen bir elektrik alan, manyetik alanda bir değişiklik yaratır.
6. Maxwell Denklemleri ve Lorentz Kuvvet Yasası, yüklü parçacıkların ve alanların hareketlerini karmaşık şekillerde değiştiren bir geri besleme döngüsü ile birlikte hareket eder.

4.5 Akımları Manyetik Alanlarla Değiştirme

Soru, çözümleri çok daha kolay hale getirecek Maxwell Denklemleri kullanılarak elektrik akımlarının manyetik alanlarla değiştirilip değiştirilemeyeceği sorusudur.

Cevap, teknik olarak, evet, bazı basit durumlarda yapabilirler ve bu genellikle manyeto-hidrodinamik teorilerde ve modellerde yapılır çünkü belirli plazma fenomenlerini incelemek için daha uygundur. Bununla birlikte, plazma davranışının, yüklü parçacıkların hareketini dikkate almanın gerekli ve önemli olduğu birçok yönü vardır, çünkü sadece alan davranışını düşünmek, plazma davranışının gözlemlenen karmaşıklığını modelleyemez.

Durum, parçacık fiziğindeki dalga-parçacık ikiliğine benzer: parçacık açıklamasını kullanmanın gerekli olduğu bazı durumlar vardır.

Parçacığın veya güncel açıklamanın kullanılmasını gerektiren plazma davranışının örnekleri arasında hücreselleştirme ve filamentleşme, enerji taşınması ve kararsızlıklar yer alır. Elektrik akımlarının ve devrelerinin dikkate alınması ayrıca parçacık tabanlı bir tanımın kullanılmasını gerektirir.

Bu durumlarda yalnızca alan etkilerini düşünmek, plazma davranışının gerçek karmaşıklığını gözden kaçıracaktır. Daha sonra bu daha karmaşık davranışlardan bazılarına bakacağız.

Merkezi plazma jeti ve sonuçta on binlerce ışıkyılı yayılan tüy yapılarıyla, Chandra tarafından X-ışını "ışığında" görülen Galaxy Centaurus A